What are properties of Liquid?

 

Chemical Kinetics

 

The study of the rate of chemical reaction, factors affecting rate of chemical reaction and mechanism of chemical reaction is called Chemical Kinetics.

Types of Chemical Reactions Based on Reaction Rate

There are three types of chemical reactions on the basis of the reaction rate.

Instantaneous Reactions

These are the reactions which are completed at once e.g. reactions between aqueous solutions of AgNO₃ and NaCl to form a white precipitate of AgCl, decolourization of acidified KMnO₄ with FeSO₄ solution.

Moderate Reactions

These are the reactions which proceed at a moderate speed. The accurate measurement of the rates of reaction is possible e.g. hydrolysis of ethyl acetate to form ethyl alcohol and acetic acid, decomposition of hydrogen iodide into hydrogen and iodine.

Slow Reaction

These are the reactions which take long time to complete, e.g. rusting of iron, fixation of atmospheric nitrogen.

 

Rate of Reaction

The rate of reaction may be defined as the change in concentration of a reactant or product per unit time. Mathematically Rate of a Chemical Reaction  =  dx / dt

Units of Reaction Rate

The units for the rate of chemical reaction are mole per cubic decimetre per second (mol. dm-3.s-1)

Rate Law or Rate Expression

The equation which describes the relationship between the concentration of the species involved and the rate of reaction, is called the rate law or rate expression.

Consider a simple reaction                A  +  B        →      Products

The rate expression for the simple reaction is written as

dx /  dt  α  [A]                 or dx / dt  =  K[A]

where ‘dx’ is the amount of substance ‘A’ changed to products in time ‘dt’, K is called the specific rate constant and [A] is the molar concentration of substance ‘A’.

 

Order of Reaction

It is defined as the sum of the powers of the concentration terms of the reactants in the rate equation.

Consider a general reaction                a A  +  b B          →      Products

Where ‘a’ is the no. of moles of substance ‘A’ and ‘b’ is the no. of moles of substance ‘B’. The rate equation for this general reaction can be written as

dx / dt  =  K[A]^m x [B]ⁿ

n + m is the order of reaction.

The values of ‘m’ and ‘n’ may or may not be equal to the no. of moles of the reactants ‘a’ and ‘b’.

The order of reaction may be equal to zero, one, two or three. 

When it is zero, the reaction is called Zero Order Reaction. The rate of a zero order reaction is independent of the concentration of the reactant(s). Example of such reactions is thermal decomposition of hydrogen iodide on gold surface.

When the order of reaction is one, it is called First Order Reaction. In first order reaction, the reaction rate depends only upon the first power of the concentration of a single reactant.

N₂O₅           →      2 NO₂  + ½ O₂

When the order of reaction is two, it is called Second Order Reaction. In second order reaction, the rate of reaction is directly proportional to the molar concentrations of two reactants. The example of second order reaction is:

2 HI →       H₂  +  I₂

CH₃COOC₂H₅  +  NaOH    → CH₃COONa  +  C₂H₅OH 

When the order of reaction is three, it is called Third Order Reaction. In third order reaction, the rate of reaction is proportional to the molar concentration of three reactants.

The order of reaction may be in fractions such as 1.5. Such reactions are called Fractional Order Reactions.

Certain reactions involve more than one molecules but these follow first order rate equation. Such reactions are called Pseudo-First Order Reactions. In these reactions, the concentration of one of the reactants, usually solvent, is present in large excess and remains constant. Example of such reactions is:

CH₃COOC₂H₅  +  H₂O             →                CH₃COOH  +  C₂H₅OH

Order of a reaction can be determined by a) Integration method (Method of trial)

b)    Half-life method

c)     Graphical method

 

Molecularity of Reaction

It is defined as the sum of no. of moles of reactants present in the balanced chemical equation of a certain reaction.

Consider a general reaction     a A  +  b B →       Products

Molecularity of the reaction  =  a  +  b

The molecularity of a reaction is always a whole number.

It may also be defined as the no. of reactant particles involved in a single collision, leading to the formation of products.

When only one molecule is involved in the collision, it is called Unimolecular Reaction. Similarly, the reactions are called Bimolecular and Trimolecular (or Termolecular) when two and three molecules are involved respectively in collision.

 

Arrhenius Equation (Effect of Temperature on Reaction Rate)

The first empirical equation to show the variation of rate constant (K) of the reaction with temperature was suggested by Hood. According to this equation

Log K  =  A′ – B/T where A′ and B are constants, T is temperature on Kelvin scale.

The values of the constant A′ and B are obtained by plotting a graph between the values of log K and 1/T when a straight line is obtained from the intercept of straight line, whereas the value of constant B is obtained from the slope of the line. The above equation in exponential form can be represented as follows:

                                        K  =  A . e^-B/T

Arrhenius in 1889 replaced the constant B by E_a and multiplied temperature with gas constant R.

The equation thus obtained is           K   =  A . e^-Ea/RT

In this equation K is specific rate constant, A is constant called frequency factor and depends on steric factor and collision frequency. It is also called Arrhenius constant, e is the symbol for the exponent, E_a is the energy of activation, R is gas constant and T is absolute temperature. The above equation in log form can be written as ln K  =  ln A . e^-Ea/RT  =  ln A  +  ln e^-Ea/RT   or   ln K  =  ln A  -  E_a /  RT Converting the natural log to log10, we get

2.303 log K  =  2.303 log A  -  E_a / RT       or      log K  =  log A – E_a / 2.303RT  Integrating the equation between the limits, we get the equation as

log K₂ / K₁  =  E_a / 2.303R [(1 / T₁) – (1 / T₂)]

The validity of Arrhenius equation can be tested by plotting a graph between log K and 1/T when a straight line is obtained. The slope of this line gives the value of -E_a / 2.303R and the intercept will give the value of ‘log A’.

 

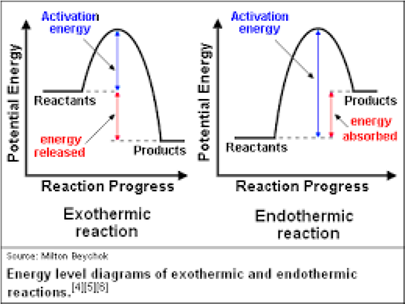
Energy of Activation

When a reaction is taking place, the reactants do not convert directly into products. Actually the reactants acquire an additional amount of energy excess to the average energy of the molecules at a given temperature. This additional amount of energy which the reactant molecules must acquire for the conversion to the products is called Energy of Activation and is denoted by E_a.

A plot of potential energy of the reactant molecules against the reaction coordinates is shown below:

 

In the form of equation, the change of reactants into products can be represented as

                    Reactants    →      Activated state     →      Products

e.g.
H --- H  +  I --- I	→      H --- H		→	2 HI
	I  ---  I
(reactants)	(activated state)			(products)

Experimental Determination 

The experimental determination of energy of activation is based on Arrhenius equation which in exponential form is written as 

K  =  Ae^-Ea/RT         or       K/A  =  e^-Ea/RT

Taking log on both sides of the equation, we get ln K/A  =  -E_a / RT or  2.303 log K/A  =  -E_a / RT or log K/A  =  -E_a / 2.303RT  or log K – log A  =  -E_a / 2.303RT or  log K  = -E_a / 2.303RT  +  log A

This is equation of straight line, representing       y = -mx + c

Where ‘m’ is the slope of straight line and ‘c’ is the intercept of the straight line.

Temperature is independent variable in this equation while rate constant k is dependent variable. The other factors like E_a, R and A are constant for a given reaction.

When a graph is plotted between 1/T on x-axis and log k on y-axis, a straight line is obtained with a negative slope. Actually, E_a / RT has negative sign, so the straight line has two ends in second and fourth quadrants. The slope of the straight line is measured by taking the tangent of that angle θ which this line makes with the x-axis. To measure the slope, draw a line parallel to x-axis and measure angle θ. Take tanθ which is slope. This slope is equal to E_a/2.303R

         

                                                          

                    Slope  =  -E_a / 2.303R    or      E_a  =  -Slope x 2.303R

The straight lines of different reactions will have different slopes and different Ea values.

The units of slope are in Kelvins (K).